Is Jayadevan's proposed method better than the Duckworth/Lewis method?
Srinivas Bhogle
It is going to be difficult to answer this question. My gut feeling is
that Jayadevan's proposed method to reset targets in interrupted limited
over international (LOI) cricket matches could indeed challenge the
Duckworth/Lewis method. But we will have to do a lot of work before we can
reach a decisive verdict.
One way to reach this verdict would be to determine objective criteria
to compare the two methods, look at a large number of examples and,
finally, simply argue. This should certainly get us somewhere.
The "objective" criteria
I can think of five criteria, perhaps in that order:
- the target set should be fair and reasonable
- calculations must be easy and understandable
- the method must handle all kinds of interruptions
- the underlying mathematical model should be theoretically valid,
internally consistent and, hopefully, even elegant
- the method must be able to handle special or unusual situations
sufficiently well.
In the following discussion we will consider each of these five
criteria. In doing so, I will draw heavily from my earlier articles on
Rediff introducing both the Duckworth/Lewis (D/L) and Jayadevan (J)
methods. I will also quote extensively from private communications which I
have received both from Duckworth and Lewis and Jayadevan.
"Fair and reasonable"
There have been over 200 applications of the D/L method in the last
four years, and I can recall only a handful of cases where the target has
been seriously questioned. This is excellent by any yardstick, but we
could still argue! For example, if the 1999 India vs Sri Lanka World Cup
match had terminated with Sri Lanka at 117 for no loss in 25 overs, in
reply to India's massive 371, Sri Lanka would have won according to the D/L method!
I cite this instance to contend that although D/L has performed
remarkably, it might also be lucky that no really "bad", albeit very
improbable, result has so far been actually encountered. But as cricket
match preparation gets more scientific, strategies could evolve to exploit
such weaknesses. If I had been advising SL in that match, I'd have said:
"Look, you can never win chasing 371. So pretend that this is a test match
and try to reach 117/0 in 25 overs. Then pray hard for rain!". [The J
method sets a winning target of 150/0 in 25 overs; a revised D/L model,
which requires the use of computers, sets a target of 152/0 in 25].
We'll return to discuss more examples of "bad" targets, using both the
J and D/L methods, a little later. But let's first look at the J and D/L
targets in more "normal" situations. Let's look at two tables comparing
the J and D/L targets. The first table looks at likely, but hypothetical,
match situations. The second table looks at real match situations.

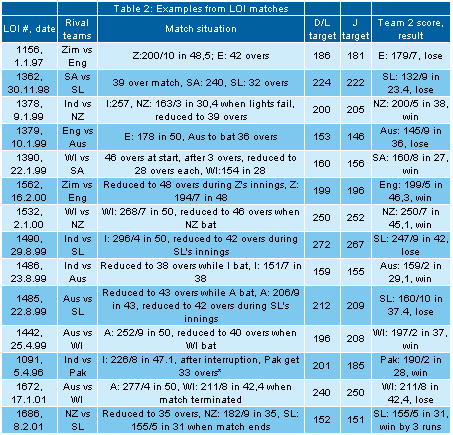
These 14 examples suggest that while the D/L and J targets are never
too far from each other; there are six cases (*) out of these 14 when
they differ by more than 10 runs.
Let's see how the comparison involving real LOI matches looks like. In
some of these matches the D/L method was not actually applied.
In the next set of 14 matches, the D/L and J targets are in much better
agreement, with only one case (*) differing by more than 10 runs. This is
re-assuring; it must seem that real matches "behave" better than
hypothetical ones! More seriously, this really means that the D/L and J
targets match very well on the average. The disagreements arise only in
more unusual or extreme situations.
It is therefore important to look at these more unusual situations. It
is my personal view that D/L targets are questionable in two situations.
The first, and this is well-documented, is when Team 2 is chasing a "well
above average" total and holding on to its wickets. In such situations,
D/L sets "well below average" winning targets for Team 2. We talked of the
extreme situation in the India vs SL match. But this anomaly persists even
in less extreme situations: With 94/0 in 25 overs, or even 115/2 in 25,
Team 2 can defeat Team 1 who have scored 300 in 50 overs.
The second questionable situation can occur in low scoring (150 or
below runs) matches where Team 1's innings has been severely curtailed.
For example, in a recent (October 2000) match between New Zealand (NZ) and
South Africa (SA), after a one-over interruption at 81/5, NZ recovered to
114/5 in 32.4 overs in difficult batting conditions when their innings was
terminated. In reply SA were asked to score 153 in 32 overs to win, i.e.
almost 40 more runs in the same 32 overs. It required the genius of Lance
Klusener to lead SA through, but did they deserve to lose if they had
scored 150/5 in 32 overs?
When I discussed these two examples with Duckworth and Lewis, they
acknowledged that the first situation does reveal a basic weakness in the
D/L model (and indicated that their revised computer-dependent model would
correct this anomaly). They however defended the D/L target in the second
situation stating that extensive analysis indicated that, on the average,
teams in situations similar to NZ's would reach around 190 in 49 overs.
So, given that SA knew their target from the start, 153 was quite a
realistic target.
I am still not fully convinced. Those who know the D/L method
sufficiently well will recognise that, in obtaining the target of 153, D/L
uses the G50 = 225 rule which assumes that, on the average, Team 2 are
expected to score 225 in an innings. In low scoring matches (usually due
to difficult batting conditions), if Team 2 appear capable of only
reaching about 150, the assumption that they will get to 225 is
significantly off the mark. It is this assumption which pushes the target
up abnormally. Put another way, if a supremely talented Klusener is
required to do his best to reach the target, the target is, generally
speaking, very unfair.
How does the J method perform in these two questionable situations? If
Team 1 score 300 in 50, Team 2 can win if they reach 122/0 in 25 (as
against D/L's 94/0) or 130/2 in 25 overs (D/L: 115/2). These targets
certainly appear more reasonable. In the second situation, the
J target for SA would be 128 in 32 overs, which, again,
appears more reasonable.
When would I want to question the J targets? I am just a little concerned about how the J model responds to the fall of wickets. In the
example above, I find it hard to accept that 122/0 and 130/2 have the same "parity" at the half-way stage; 122/0 is distinctly more comfortable!
To study how J targets vary with the fall of wickets, let's consider
the situation where Team 1 score 125 in 25 overs when a heavy downpour
causes the match to be curtailed to 25 overs per side. We'll tabulate Team
2's target in 25 overs for all possible "loss of wicket" situations.
| Table
3 |
|
|
| Team 1's end
score |
D/L
target |
J
target |
| 125/0 |
210 |
197 |
| 125/1 |
203 |
191 |
| 125/2 |
194 |
185 |
| 125/3 |
184 |
179 |
| 125/4 |
170 |
153 |
| 125/5 |
153 |
133 |
| 125/6 |
134 |
126 |
| 125/7 |
116 |
126 |
| 125/8 |
103 |
126 |
| 125/9 |
93 |
126 |
Table 3 indicates that while the D/L target reduces after the fall of every wicket (and very steadily), the variation of J's targets with the fall of wickets is less smooth and a trifle "sluggish". Jayadevan doesn't agree with this reaction (and counters that D/L is "over-responsive" to the fall of wickets), but I still consider D/L's fall-of-wickets "distribution" to be superior especially when the last few wickets are batting.
Notice also how the D/L target falls below 125 from 125/7 onwards. This
lower target for Team 2, in the same number of overs, initially
surprised me, but it is entirely consistent with the D/L philosophy of
compensating the team that has fewer resources. J, on the other hand, does
not allow a smaller target for Team 2 in the same number of overs partly because he believes that the cricket fan will not
accept this situation.
"Easy and understandable calculations"
Jayadevan told me recently that many Indian umpires couldn't set a D/L
target without some help. This is surprising because the D/L method is
really quite simple. If this is indeed the case, umpires will also have
trouble with the J method, especially in situations involving multiple
interruptions.
It is my considered view that a target resetting method need not be
unnecessarily simple, especially if this requirement weakens the
method. But every cricket person I know talks of that "perfect method"
which is both very easy to understand and work out, and also sets
impeccable targets in all situations. This is a pipe dream. Both the D/L
and J methods suffer marginally because of this forced requirement of
being "easy to calculate". I personally advocate the use of the most
sophisticated available method, even if it needs a computer. But this
isn't a very popular prescription! My friend Vidyadhar Mudkavi has an even
better suggestion: build cheap, attractive and portable D/L or J
calculators in which the target resetting computer programs are "hard
coded". This would solve everyone's problem!
To return to our D/L vs J comparison, a calculation using either method
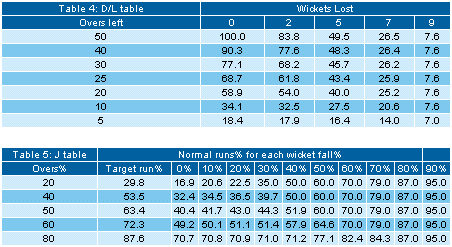
is really no big deal. It essentially involve looking up tables (see
typical extracts in Tables 4,5), noting down a few values "on the back of
the envelope" and then doing some simple arithmetic.
The tricky part is to decide what to look up from the table. My
experience, after a few hundred calculations using the D/L and J methods,
is that the J method is marginally simpler for situations involving only a
single interruption. For multiple interruptions, however, D/L is significantly simpler.
I have also found it just a shade difficult to explain the D/L method
to the layman, chiefly because it takes a little while to explain the
abstract idea of a "resource percentage" (RP). D/L calculations also
involve a moment's confusion between "RP available" and "RP used". With
the J method, there is the overhead of converting balls remaining in an
over into a percentage. Since J currently doesn't have a ball-by-ball
percentage table for overs% and runs%, we are also required to do some
trivial interpolation.
Both the D/L and J methods are capable of calculating the
winning target on a ball-to-ball basis when Team 2 is chasing its
victory target; but the D/L method is better suited for such a calculation. In a recent LOI match (see last row of Table 2) between
Sri Lanka (SL) and New Zealand (NZ), SL, chasing 183 in 35 overs, had
reached 155/5 in 31 overs when the rain returned to end the match. For a
moment, no one knew who had won! A D/L calculation eventually declared SL
winners by 3 runs. The confusion arose because neither team kept track of the winning score on a ball-to-ball basis.
"Handle all interruptions"
An essential requirement of LOI target resetting methods is the ability
to handle all kinds of match interruptions. We could divide
interruptions into five types: (a) interruption between Team 1 and Team
2's innings, (b) single interruption while Team 2 are batting, (c) single
interruption while Team 1 are batting, (d) more than one interruption
while Team 2 are batting and (e) more than one interruption while Team 1
are batting.
Before the D/L method came along in 1998, only the first two types --
type (a) and type (b) -- of interruptions could be handled sufficiently
well. Interruptions while Team 1 are batting -- type (c) and type (e) --
were not even "recognised"; the accepted practice was that if Team 1 got
to play 30 overs, after one or more stoppages, and scored 120 runs, Team 2
would need to get 121 in 30 overs. This severely disadvantaged Team 1; and
so encouraged the popular practice of always inviting the opposition to
bat first on a wet day.
Duckworth and Lewis changed all that and completely solved the problem
of handling multiple interruptions. I remember writing about it in 1999,
and I still consider the greatest merit of D/L to be this ability to
handle multiple interruptions. No method can possibly improve D/L's
procedure for dealing with multiple interruptions. In fact the D/L method
tends to treat single interruptions as a special case of its multiple
interruption rule.
The J method must therefore pass the difficult test of first
demonstrating its capability of handling all the five types of
interruptions, and then showing that it can match D/L's acknowledged
prowess in handling interruptions.
The J method, especially after Jayadevan's recent revision, can now handle all the five interruption types. His method performs well, and is
certainly on a par with D/L, while handling single interruptions. J's
procedures for multiple interruptions work equally well; but they are not as
"natural" as D/L.
"Good mathematical model"
I remember receiving a mail from Duckworth and Lewis asking if the J
method was based on firm mathematical principles. It is, although the J
and D/L equations are very different. Both methods use average scoring
patterns; D/L derives its target from an exponential relationship
while J uses a regression fit.
One major difference between D/L and J lies in the way the methods
respond to the fall of wickets. Generally speaking, D/L resets targets,
after the fall of each wicket, exceedingly well, although its targets tend
to be low till the first couple of wickets fall. J, as we have remarked,
is much less responsive to the fall of wickets.
After a first tutorial on the D/L method, the most frequently asked
question is why D/L has different target resetting rules for the "R1 >
R2" and "R2 > R1" situations. If the ratio of the resources can be used
to "scale down" targets, why not to "scale up" targets? One of the merits
of the J method is that it can both "scale up" and "scale down" using the
ratio of the same variables. This offers J the additional advantage of ensuring
that Team 2's target is always proportional to Team 1's score.
In its early versions, the J method contained several technical anomalies, most of them identified by D and L. After his recent revision, Jayadevan is now confident that all anomalous situations have been corrected.
"Handle special situations"
LOI matches, especially those played in India, Pakistan, SL and
Bangladesh, now have two very high scoring phases: the first 15 overs --
to exploit field restrictions -- and the last 5-10 overs. While the D/L
model is "well-prepared" for the end innings slog, people have often asked
if D/L is equally well prepared for the first 15-over slog. D and L
maintain that all available statistical evidence suggests that the higher
scoring is adequately compensated by the more probable loss of (more
valuable) wickets. The J model, on the other hand, recognises and
accommodates the expected early slog.
In matches where a penalty is imposed for a poor over rate, the D/L
method has to make an awkward correction in the RP available value. The J
method, which is based on the overs percentage, has no such
problem.
Winding up
It is now time to take stock and see if we can reach a verdict on D/L
vs J. Just to make things simpler for all of us, let me put down the
principal arguments for each of the five criteria in Table 6.
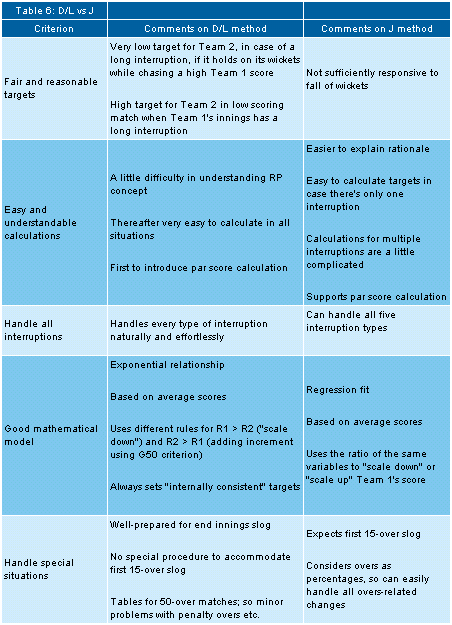
I think that Table 6 is quite useful. Each one of us can make our own
comparative assessment based on the importance that we would like to
attach to each criterion, and the related arguments. Individual
assessments could point either to D/L or J; this won't surprise me,
because both are worthy methods.
Who would I vote for? I have been trying to put off this question to
the very end, but, if I am asked to judge, I would raise my finger for
Jayadevan. If this looks like an Indian umpire upholding an Indian
bowler's appeal, then so be it!
Acknowledgements
It gives me very great pleasure to thank Frank Duckworth, Tony Lewis
and V Jayadevan for being so very helpful in helping me prepare this
article. We have exchanged dozens of e-mails between ourselves over the last 6-8
weeks. I thought it was absolutely wonderful of D and L to share so much
information with us, although they were well aware that Jayadevan could go
on to challenge their own method. I must also thank Prem Panicker and
Rediff once again. It is satisfying to note that all my three articles now
appear on what I consider to be India's best website.
Jayadevan's rain rules for LOI cricket
Also read: The dummy's guide to Duckworth-Lewis
Srinivas Bhogle is Scientist and Head, Information Management
Division, National Aerospace Laboratories, Bangalore, India.