|
|
| Help | |
| You are here: Rediff Home » India » Get Ahead » Careers » Education |
|
| |||||||||||||||||||||||
|
| |||||||||||||||||||||||
Most of our tenth graders find geometry a hard nut to crack. They face difficulty in proving certain results in a given geometric figure. It is not because they do not know the basic rules and formulas. Most times, the difficulty is in understanding the question and then finding the right strategy to prove the required result.
Sometimes, to solve a problem you may have to use multiple relationships and such questions are a bit confusing and therefore challenging. Experts from TCYonline.com present for the readers of rediff.com some useful tips and traps in Geometry.
Let's see how we can master some techniques in order to act speedily as well as accurately.
Master the art of 'marking'
At the Class X level, most questions from Geometry include a figure. However, in case the figure is not given, your first task is to create a figure that reflects the facts given in the question. The best and easier way to do that is by using a consistent system of "markings" to represent facts given in the question.
For instance, in the figure below, ABC is a triangle with AB = AC.
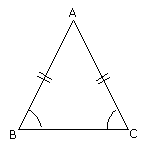
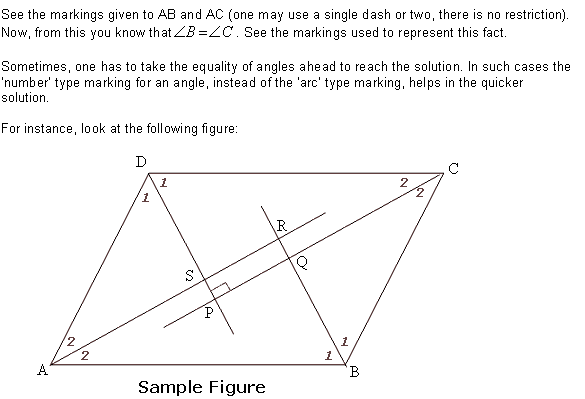
Here it is given that ABCD is a parallelogram and interior angle bisector to all the four angles are drawn intersecting are P, Q, R and S making another quadrilateral. We have to prove that PQRS is a rectangle.

Master the art of 'analysis'
You really need to master the art of analyzing a problem from Geometry. First step is to find out exactly what is asked in the question. You may be asked to
- find the length of a side
- find the diameter of a circle
- prove a particular result, etc.
There are always two ways to solve:
1. Given information + Some logical reasoning = Solution
2. Given information + Some additional information + Some logical reasoning = Solution
For Instance, let us take the same example (Sample figure given above) to explain. Here are the steps for analysis:
1. Plan backwards: We need to prove that PQRS is a rectangle, which is possible if we prove that all angles i.e. P, Q, R, S are 90 degrees or at least opposite angles ie (P, R) or (Q, S) are 90 degrees.
2. Recall the factual Information: Here, the additional information is nothing but the FACTS about parallelograms and rectangles given above only.
3. Use markings: As explained above.
4. Present the answer: The solution must be presented in the standard format and must be properly explained by mentioning the theorems used. 1s and 2s in marking is just a way to reach the solution. Prefer using the complete names of the angles in writing the answer.
Master the art of 'construction'
In the second situation mentioned in the "analysis" part, you find that some additional information is required to solve the problem. In such a situation you need to go for a construction.
For instance, look at the following situation:
ABCD is a parallelogram. �BAD = 30�, BA = 6 cm and AD = 12 cm. What is the area of ABCD?

Now, it is clear that to find the area of the parallelogram you need the height and no height is given in the figure. This means the available information is not sufficient. We need some additional information ie the height. Now you will go for a construction, as shown below.
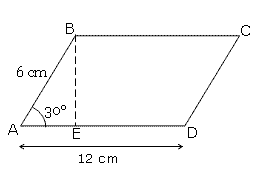
To solve a geometry problem you have to go through all the above steps.
Now, some readymade material will be of great help to solve many questions in geometry. If you have such a material, it will flash in your mind when you analyze a question. This flash will, more often than not, take you to a relationship that will help you solve the problem. Let us try to generate a few flashbacks from the concepts involved in our syllabus.
Know the most common errors
~ Using BPT (Basic Proportionality Theorem): Make sure you use BPT ONLY when a line parallel to one side of a triangle intersects the other two sides of the triangle. That is, if the intersecting line is not parallel to the third side, you cannot apply BPT.
For instance, look at the following figure:
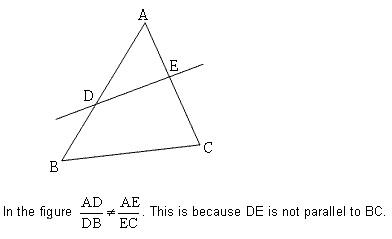
~ Simplifying the Complex problems: Most of the time a lot of triangles are given in the figure and we often get confused as to what to refer and what to avoid.
For instance, look at the following figure:



~ Understanding correspondence in similar triangles: For instance, look at the following figure:

Remember, the three options are all different and writing any one will be a blunder in the examination. Here is a simple way to do it:
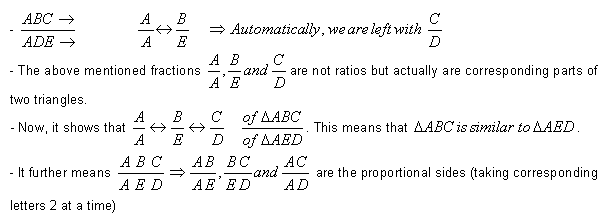
- 7 tips to finish your maths paper before time
- 9 most common maths mistakes
- Geometry and statistics simplified!
- Speed strategies in mathematics for class X
- Parents keep exam stress at bay!
- How to make mock tests work for you
- Taming mathematics
- Class X: All about the new pattern
- Class X board exams: Preparation tips
|
|
| © 2008 Rediff.com India Limited. All Rights Reserved. Disclaimer | Feedback |